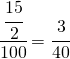Percentage
The phrase per cent is formed of two words – per and cent. Per means out of and Cent means hundred. Thus, per cent means out of hundred. For example, 8 per cent means 8 out of hundred. The symbol for per cent is ‘%’. 15% means 15 out of 100 and is equivalent to
Difference between Percentage and Percent:
The word percentage and percent are closely related to each other. Percent ( or symbol %) is accompanied with a specific number such as 55%. Percentage is represented without a number, is used generally for general case of percent.
How to convert Per Cent into an Equivalent Fraction
Example 1:
Convert 50% into an equivalent fraction.
50% =
Example 2:
Convert 75% into an equivalent fraction.
75% =
Example 3:
Convert 5 % into an equivalent fraction.
5 % =
How to convert a Fraction into an Equivalent Per Cent
To convert a fraction into an equivalent per cent, multiply both the numerator and the denominator by such number so that the denominator becomes 100 OR multiply the given fraction by 100 and put the symbol % after the product. See the examples given below for better understanding.
Example 1:
Convert into an equivalent per cent.
= 40%
OR
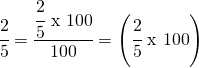
Example 2:
Convert 5 into an equivalent fraction.
5 = 625%
OR
5 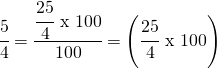
How to convert Decimal into Per Cent
To convert a decimal into an equivalent per cent, multiply both the numerator and the denominator by such number so that the denominator becomes 100 OR multiply the given fraction by 100 and put the symbol % after the product. See the examples given below for better understanding.
Example 1:
Convert 0.5 into its equivalent per cent.
0.5 = = 50%
OR
0.5 = % = 50%
Example 2:
Convert 4.5 into its equivalent per cent.
4.5 = = 450%
OR
4.5 = % = 450%
How to convert Per Cent into Decimal
To convert a per cent into an equivalent decimal, change the per cent into a fraction and then to decimal. See the examples given below for better understanding.
Example 1:
Convert 25% into decimal.
25% = = 0.25
Example 2:
Convert 70% into decimal.
70% = = 0.70 = 0.7
Example 3:
Convert 4% into decimal.
4% = = 0.04
Example 4:
Convert 127% into decimal.
127% = = 1.27
Click on Next button to see solved examples on the chapter Percentage for Class 5 Mathematics.
Solved Examples
Example 1:
Find the value of 5% of 100.
5% =
5% of 100 =
Example 2:
Find the value of 25% of 200.
25% of 200 =
Example 3:
Which is more: 20% of 300 or 25% of 200?
20% of 300 =
25% of 200 =
Since, 60 is greater than 50
So, 20% of 300 is greater than 25% of 200
Example 4:
Which is greater: or 6%
6% =
Now we have to compare and
First we have to make them equivalent fraction,
Since, >
Therefore, > 6%
OR
= 0.6
6% = = 0.06
On comparing 0.6 and 0.06
We get 0.6 > 0.06
Therefore, > 6%
Example 5:
Which is greater: 67% or 6.7?
67% = = 0.67
On comparing 0.67 and 6.7
We get 6.7 > 0.67
Therefore 6.7 > 67%
Example 6:
Rohan scored 80 marks out of 100 in Science subject. Find the per cent marks he get in Science.
Required per cent = x 100% = 80%
Example 7:
Sanjana scored 30 marks out of 50 in Maths subject. Find the per cent marks she get in Maths.
Required per cent = x 100% = 60%
Example 8:
What per cent is 30 minutes of 1 hour?
1 hour = 60 minutes
Required per cent = x 100% = 50%
Example 9:
What per cent is 1 kg 500 g of 5 kg?
1 kg 500 g = 1000 g + 500 g = 1500 g
5 kg = 5000 g
Required per cent = x 100% = 30%
Example 10:
Rohan’s salary is Rs 12000 per month. Every month he spends 75% of his salary. How much does he spend every month.
Rohan spends = 75% of salary = 75% of Rs 12000 = x 12000 = Rs 9000
Therefore, Rohan spends Rs 9000 every month.
Some more important topics of CLASS 5